Application of Bayesian inference to heavy-ion collisions

Many problems in high-energy nuclear physics can be thought of as statistical inference problems, i.e., to extract key physical parameters with quantified uncertainty from experimental data using theoretical models. The state-of-the-art theoretical descriptions often involve complicated modeling that has

1. a high-dimensional parameter space,
2. non-trivial correlations between parameters and the predicted observables,
3. various sources of theoretical uncertainties.

These problems have motivated us to go beyond eye-ball fits or even traditional (\xi^2)-fitting methods. Over the past decade, emulator-assisted Bayesian analysis has proven to be a promising solution. The use of Gaussian Process-based model emulators and dimensional reduction tools such as principal component analysis make such an approach possible for computationally intensive physical models.

Here I introduce some developments of the Bayesian analysis framework in several of my past and ongoing projects, including collaborative works within the JETSCAPE Collaboration.

Model uncertainty and Bayesian model averaging

The inclusion of theoretical/model uncertainty in statistical inference is important.

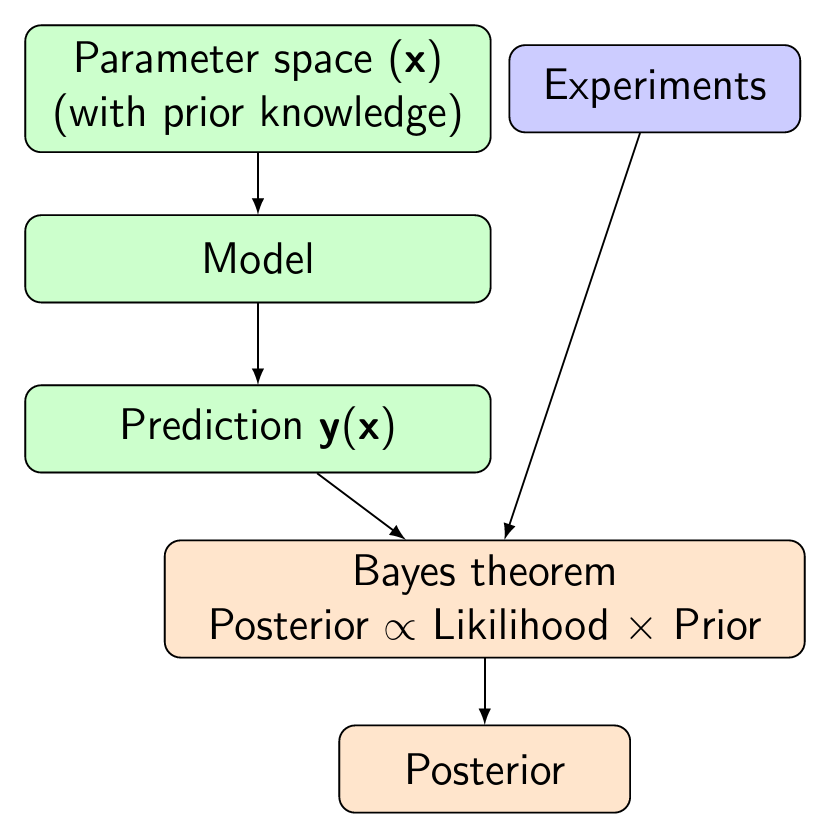
In the Bayesian methodology, distribution of the true value of parameters (P(x_i)) is the production both the experimental likelihood ( L(y_{model}(x_i) , y_{exp}, \Sigma_{error}) ) and the prior distribution (P_0(x_i)), known as the Bayes’ Theorem (()up to a normalization called the “Evidence”()). Many model uncertainties can be thought of as unknown parameters that are not of immediate interest (()nuisance parameter()). Such uncertainty can be directly folded into the posterior distribution of the interested parameter by “marginalization”, i.e., integrating out nuisance parameters in the posterior distribution ( P(x_j) = \int \prod_{i\neq j} d x_j P(x_i) ).

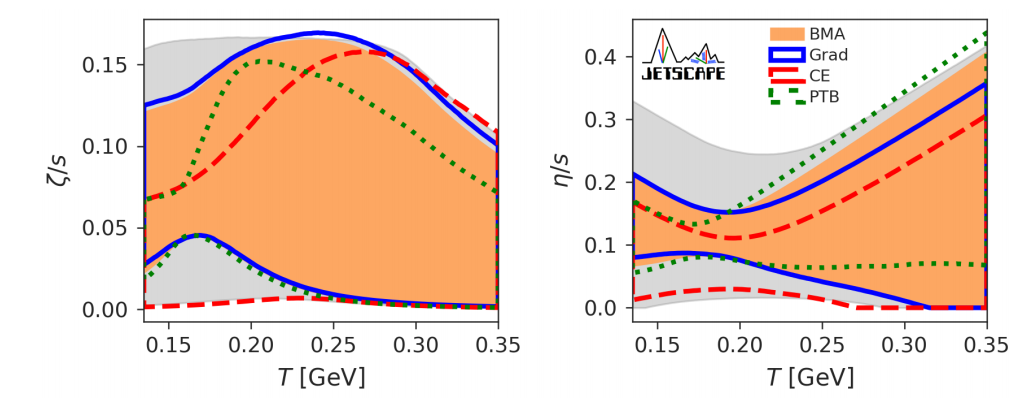Another class of theoretical uncertainty arises with different choices of modeling, e.g., different fundamental assumptions and different approximation schemes. Usually, it is better to let data tell which choice is preferred. In our recent publications within the JETSCAPE Collaboration, we accounted for the uncertainty from using different participations schemes from a hydrodynamic description to the transport description. Treating the Bayes evidence as the weight of a model, we perform a Bayesian model averaging over the posterior of the extracted shear and bulk viscosities from each model choice. It was shown that different model choices contribute a large fraction of the resulting uncertainty; however, this is an important practice to arrive at the most reliable determination of the QGP transport coefficients.

Inference of unknown functions

Often we are faced with the inference of unknown functions—objects with infinite degrees of freedom. For example, specific shear and bulk viscosity of the quark-gluon plasma as a function of temperature, jet transport parameter as a function of both the medium energy scale (() (T) or (Q_s) ()) and jet energy scale (() (E) and (Q), etc()). In the traditional ways, one parametrizes unknown functions using explicit forms with a fixed number of parameters. Then, perform statistical inference on these parameters. Finally, convert the parameters’ posterior into the posterior of the interesting function. However, the form of the parametrization is a strong assumption of the prior distribution and often introduces rather non-linearly correlations with the predicted observables. Further, such a method soon becomes untractable with higher-dimensional functions.

Recently, we use the Gaussian Process (()GP()), a class of non-parametric random functions, to represent the unknown functional space. It brings several advantages:

1. A reasonable prior:
   1. Smooth functions with smoothness controlled by hyperparameters of the GP.
   2. Functional value decorrelates over the large gap in input parameter: data that are only sensitive to function values in certain input regions will not affect those in other regions.
2. Straightforward extension to a higher dimension.
3. The prior is essentially a path integral over an infinite number of degrees of freedom. For certain problems, one can also borrow techniques of field theory. See information field theory (()IFT())

We are currently working on a first publication that applies this idea to the extraction of the temperature dependence of the jet transport parameter of the QGP. Stay tuned!

Random functions as prior	Posterior

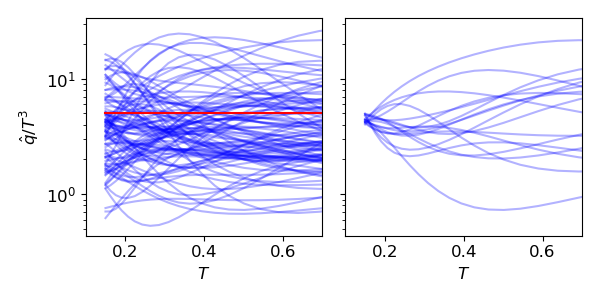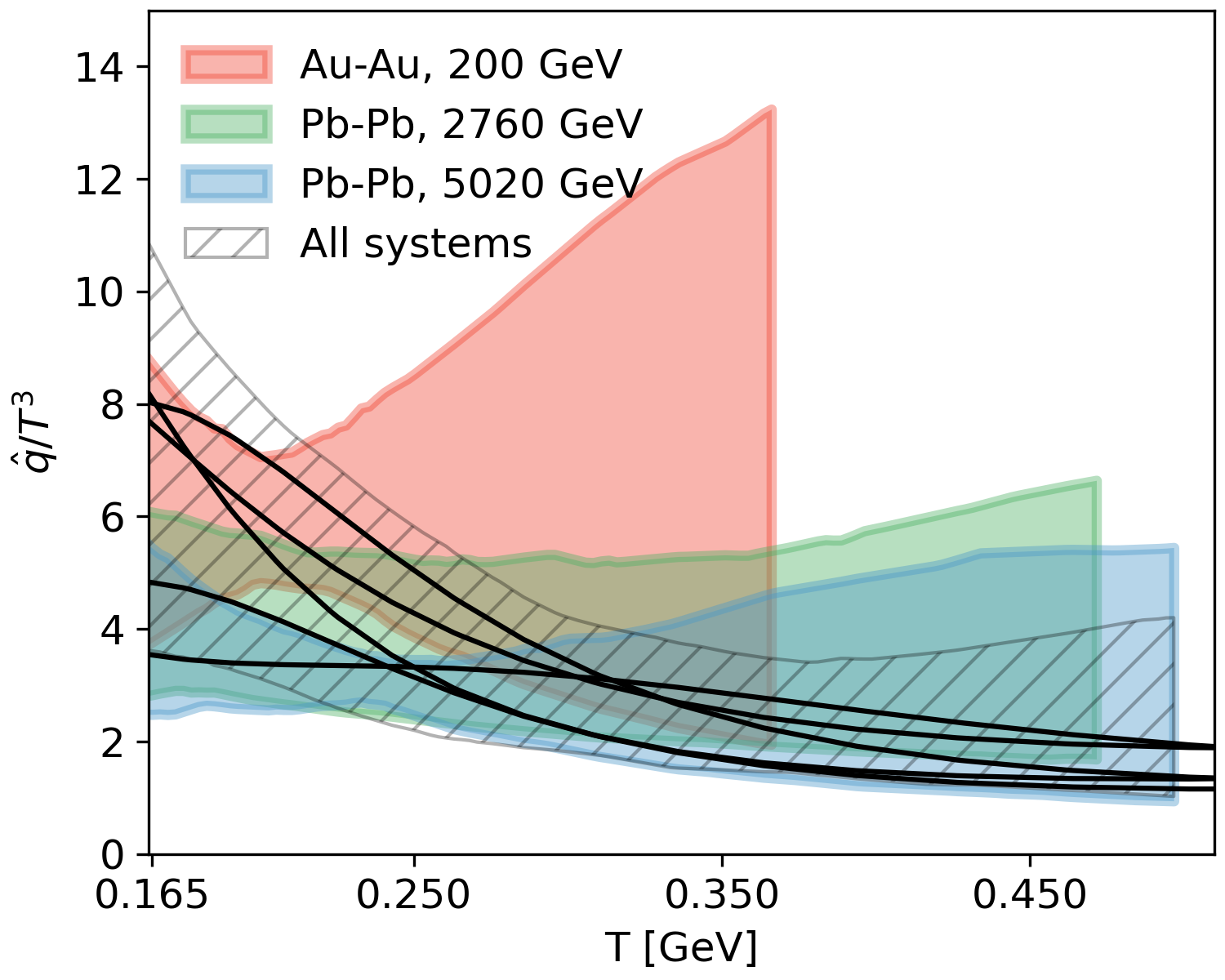Notice that the posterior represented by the red band only uses the Au-Au 200 GeV data. One does not expect collisions at this beam energy can probe the high-temperature region. This is indeed the case using the Gaussian Process as functional prior that data sensitive to low temperature does not constrain (\hat{q}(T)) in the high-temperature region as a result of the previously listed advantages 1.2.